两个谬一样的三角形为什么少了一块？附解题方法大全

  一个在网络上流传了很多年的智力题，2个面积一样的三角形进行过一次重构之后尽然少了一块，这是怎么回事，来看看。

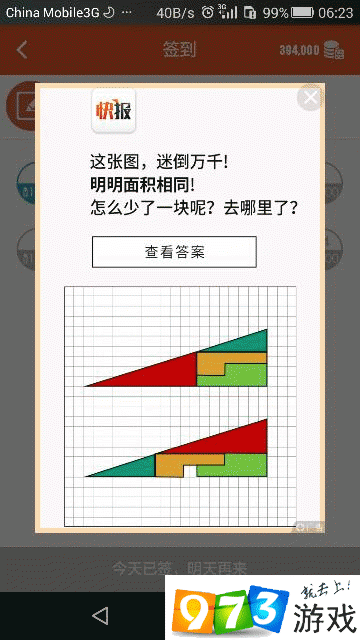
  原理

  观察此图你会发现，第一幅图的蓝绿色三角形和红色三角形的斜边并不在同一条直线上，所以第一幅图并不是一个三角形，斜率不同。 同理，第二幅图的蓝绿色三角形和红色三角形斜边也不在一条直线上。

  解法一：

  图中红色三角形斜边与水平夹角是arctg(3/8),而绿色三角形斜边与水平夹角是arctg((2/5),这两个角的不相等的,所以最上的图中,红色三角形与绿色三角形的斜边所组成的线是(交点)向下凹的两条直线,而不是一条直线,而最下的图中,红色三角形与绿色三角形的斜边所组成的线是(交点)向上凸的两条直线,这向下凹与向上凸之间所含的面积即为下图多出的方格面积追问：

  设方格边长为1,由上述分析可知,下凹与向上凸之间是组成一个平行四边形,且边长为√72和√72(即红色三角形与绿色三角形的斜边长),而这两边夹角是α=arctg(2/5)-arctg(3/8),所以平行四边形面积是：S=(√72*√29*sin(α))/2*2=√72*√29*sin(α),利用两角差的三角公式可得sin(α)=(2/√29)*(8/√72)-(5/√29)*(3/√72)=1/(√29*72),则S=√72*√29*1/(√29*72)=1,即所求面积为1个方格的面积!

  解法二：

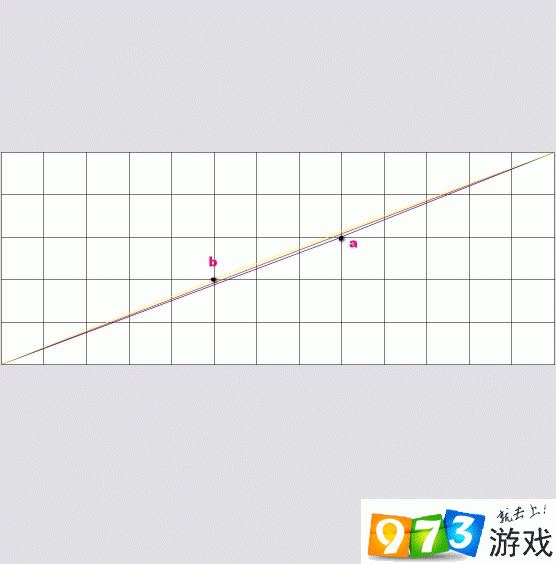
  a点为分割时的交点，红线与蓝线为比原来减少的面积

  b点为拼搭时的交点，红线与黄线为比原来增大的面积

  通过相似三角形的计算可以得到减少了5/10，增大了5/10，正好是1